Robust and scalable PCA using Grassmann averages
2014-06-01
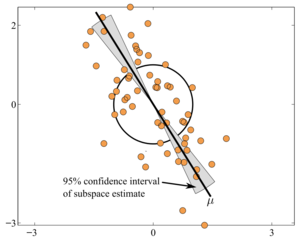
The Grassmann Averages PCA is a method for extracting the principal components from a sets of vectors, with the nice following properties: 1) it is of linear complexity wrt. the dimension of the vectors and the size of the data, which makes the method highly scalable, 2) It is more robust to outliers than PCA in the sense that it minimizes an L1 norm instead of the L2 norm of the standard PCA.
It comes with two variants: 1) the standard computation, that coincides with the PCA for normally distributed data, also referred to as the GA, 2) a trimmed variant, that is more robust to outliers, referred to the TGA.
We provide implementations for the Grassmann Average, the Trimmed Grassmann Average, and the Grassmann Median. The simplest is the Matlab implementation used in the CVPR 2014 paper, but we also provide a faster C++ implementation, which can be used either directly from C++ or through a Matlab wrapper interface.
The repository contains the following:
| Author(s): | Soren Hauberg, Raffi Enficiaud |
| Department(s): |
Perceiving Systems Software Workshop |
| Research Projects(s): |
Robust PCA |
| Publication(s): |
Scalable Robust Principal Component Analysis using {Grassmann} Averages
Grassmann Averages for Scalable Robust {PCA} |
| Authors: | Soren Hauberg, Raffi Enficiaud |
| Maintainers: | Raffi Enficiaud |
| Release Date: | 2014-06-01 |
| License: | The 3-Clause BSD License (BSD-3-Clause) |
| Repository: | https://github.com/MPI-IS/Grassmann-Averages-PCA |