Departments
- Autonomous Motion
- Empirical Inference
- Haptic Intelligence
- Modern Magnetic Systems
- Perceiving Systems
- Physical Intelligence
- Robotic Materials
- Social Foundations of Computation
- Theory of Inhomogeneous Condensed Matter
Research Groups
- Autonomous Vision
- Autonomous Learning
- Bioinspired Autonomous Miniature Robots
- Biomimetic Materials and Machines
- Dynamic Locomotion
- Embodied Vision
- Human Aspects of Machine Learning
- Intelligent Control Systems
- Learning and Dynamical Systems
- Locomotion in Biorobotic and Somatic Systems
- Micro, Nano, and Molecular Systems
- Movement Generation and Control
- Neural Capture and Synthesis
- Organizational Leadership and Diversity
- Physics for Inference and Optimization
- Probabilistic Learning Group
- Probabilistic Numerics
- Rationality Enhancement
- Robust Machine Learning
- Nanorobotic Biosensors
- Smart Nanoplasmonics
Publication Type
- Article
- Bachelor Thesis
- Book
- Book Chapter
- Conference Paper
- MPI Year Book
- Manual
- Master Thesis
- Miscellaneous
- Patent
- Ph.D. Thesis
- Poster
- Proceedings
- Talk
- Technical Report
- Thesis
- Unpublished
1 result
(View BibTeX file of all listed publications)
2023
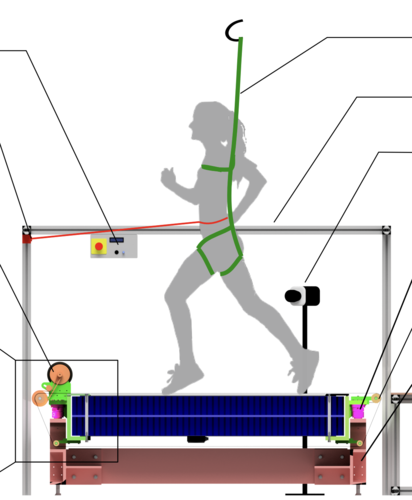
An Open-Source Modular Treadmill for Dynamic Force Measurement with Load Dependant Range Adjustment
Sarvestani, A., Ruppert, F., Badri-Spröwitz, A.
2023 (unpublished) Submitted
Ground reaction force sensing is one of the key
components of gait analysis in legged locomotion research. To
measure continuous force data during locomotion, we present a
novel compound instrumented treadmill design. The treadmill is
1.7 m long, with a natural frequency of 170 Hz and an adjustable
range that can be used for humans and small robots alike. Here,
we present the treadmill’s design methodology and characterize it
in its natural frequency, noise behavior and real-life performance.
Additionally, we apply an ISO 376 norm conform calibration
procedure for all spatial force directions and center of pressure
position. We achieve a force accuracy of ≤ 5.6 N for the ground
reaction forces and ≤ 13 mm in center of pressure position.
dlg
2023
dlg
Sarvestani, A., Ruppert, F., Badri-Spröwitz, A.
An Open-Source Modular Treadmill for Dynamic Force Measurement with Load Dependant Range Adjustment
2023 (unpublished) Submitted